No Clear Interpretation
A Mind-Blowing Math Hack

Just The Facts

DOFPro Team

Introduction

  • Discusses the basics of nonlinear interpolation in a table
  • Before the age of readily available computers most engineering data were only available as tabulations.
  • Data tables still find extensive use.

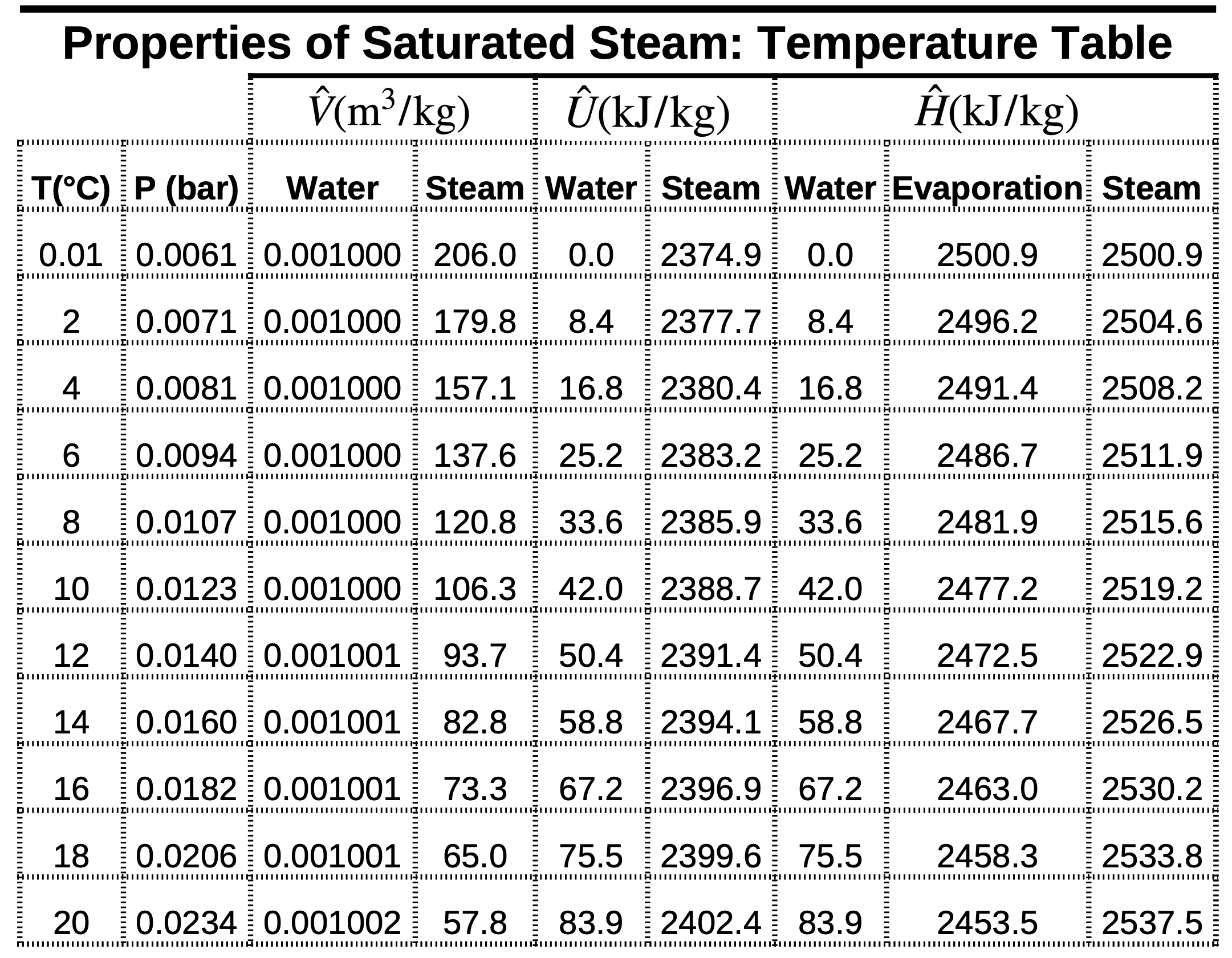
Properties of Saturated Steam: Temperature Table

Nonlinear Interpolation

Saturated Steam: Temperature Table, Pressure Column

Polynomial Interpolation

  • 2nd Order
  • 3rd Order
  • 4th Order

Cubic Spline Interpolation

Variable Transformation

Change of Variable \(\log p^*\) vs \(1/T\)

Saturated Steam: Temperature Table, Pressure Column

Use table value at \(10\ ^\circ \mathrm{C}\ (0.0123)\) as true value.

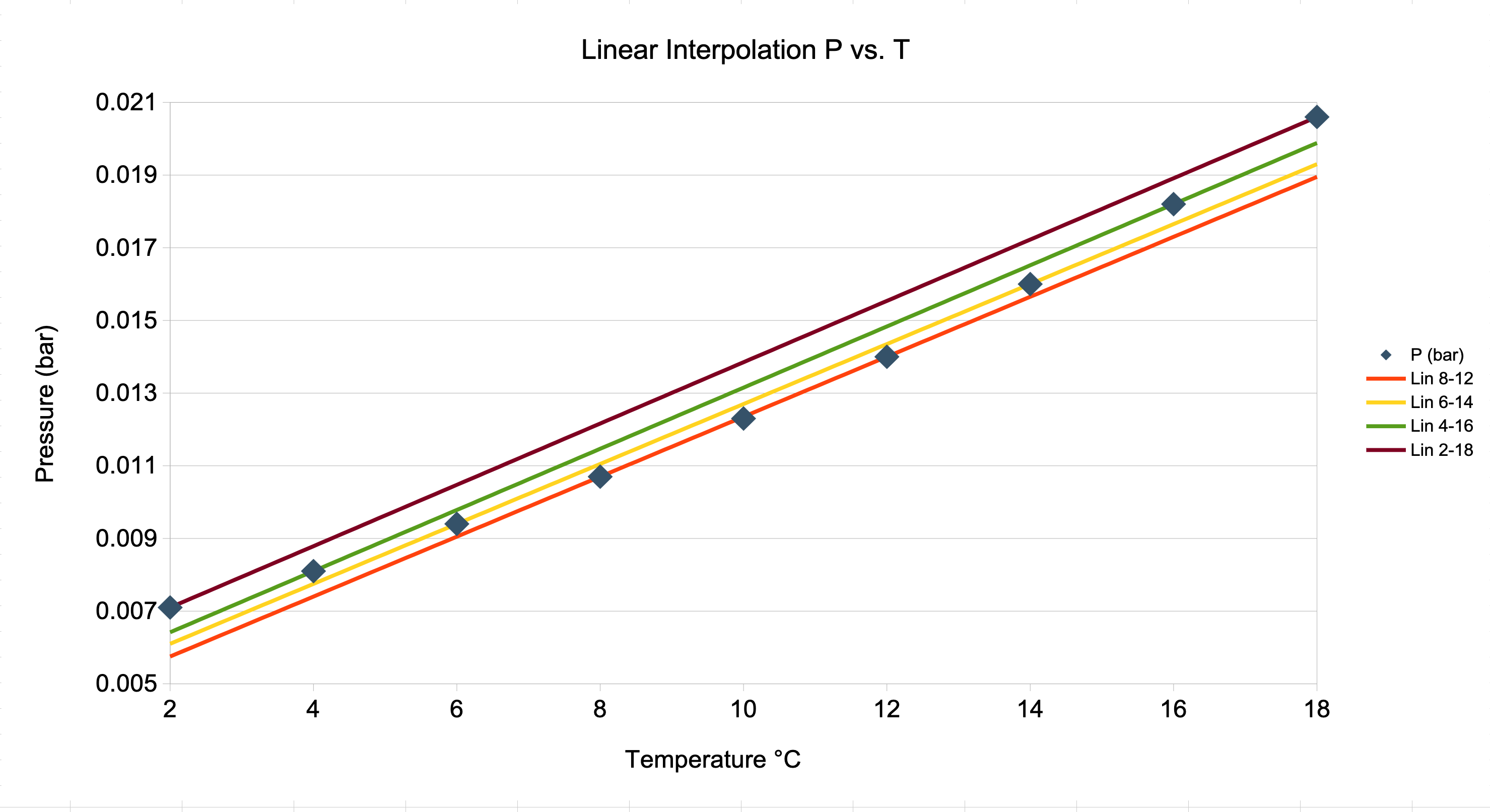
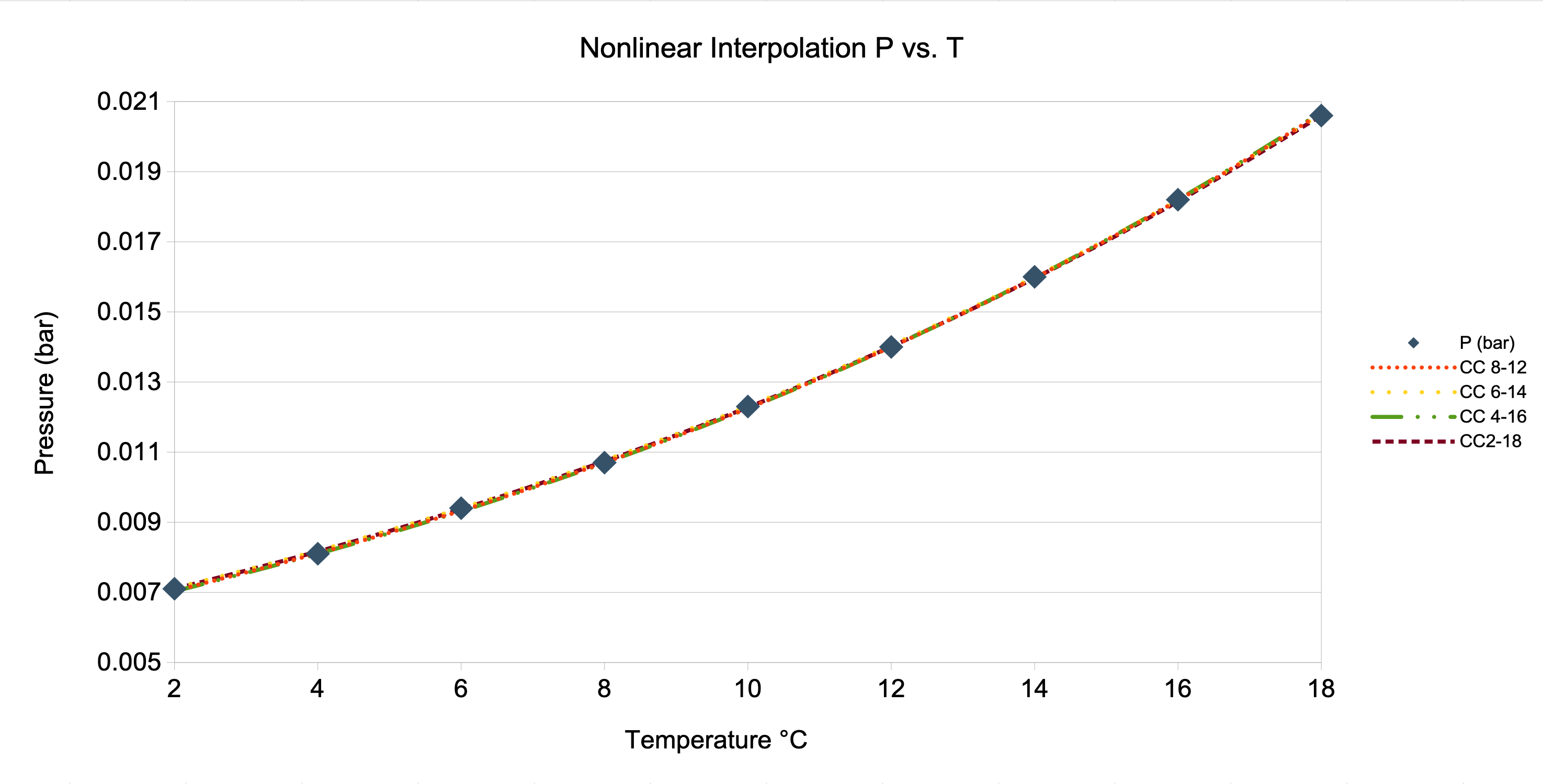
Linearly interpolate on \(p^*\) and \(T\ (^\circ \mathrm{C})\) and compare with linear interpolation on \(\ln p^*\) and \(1/T\ (\mathrm{K})\). Interpolate with endpoints at

  • \(8\ ^\circ \mathrm{C}\) and \(12\ ^\circ \mathrm{C}\)
  • \(6\ ^\circ \mathrm{C}\) and \(14\ ^\circ \mathrm{C}\)
  • \(4\ ^\circ \mathrm{C}\) and \(16\ ^\circ \mathrm{C}\)
  • \(2\ ^\circ \mathrm{C}\) and \(18\ ^\circ \mathrm{C}\)

Interpolation Fit Plots

The Takeaways

  1. Linear interpolation is adequate with closely spaced tables or low accuracy requirements.
  2. Higher-order interpolation requires more than two data points.
  3. If you have an approximate model for your table data, a change of variables can greatly increase the accuracy of your interpolation.
  4. Having a program or an app with the full model is better than interpolating in a table.






Thanks for watching!
The Full Story companion video is in the link in the upper left. The next video in the series is in the upper right. To learn more about Chemical and Thermal Processes, visit the website linked in the description to find previous and following videos in this series.

The DOFPro Team